<JIKS칼럼>
한붓그리기는 붓을 종이 위에서 떼지 않고. 같은 길을 두 번 지나지 않으면서 어떤 도형을 한 번에 그릴 수 있는 문제이다. 그렇다면 다음 한붓그리기 문제를 함께 해결해보자.
사실 위의 한 붓 그리기 문제는 답이 없다. 주어진 도형에서 꼭짓점과 변으로 이루어진 차수를 확인해보면 한붓그리기 문제의 정답을 금방 파악할 수 있다.
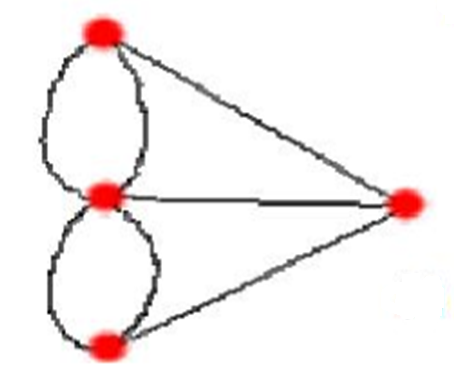
한 꼭짓점에 연결된 변의 개수가 홀수 개이면 그 점을 홀수점이라 하자. 나아가 한 꼭짓점에 연결된 변의 개수가 짝수 개이면 그 점을 짝수점이라 할 수 있다. 가령 아래 <도형1>은 모든 꼭짓점이 짝수개의 변으로 연결되어 있으므로 홀수점이 0개인 도형이다. 또 아래 <도형2>은 홀수점이 2개, 짝수점이 2개로 이루어진 도형이다.
한붓그리기가 가능한 도형은 이처럼 홀수점이 0개 이거나 혹은 홀수점이 2개로만 이루어진 도형일 때만 가능하다. 아이에게 한붓그리기 문제를 소개할 때 다음과 같은 순서로 제시하면 좋다.
1. 오일러 다리 문제 제시 / 한붓그리기가 안 되는 이유 함께 생각해보기
2. 난이도가 쉬운 한붓그리기 문제 제시 (위의 도형1, 도형2 제시)
3. 한붓그리기가 되는 조건 찾아보기 (홀수점 0개 혹은 2개일때)
4. 맨 처음에 제시한 오일러 다리 문제에서 한붓그리기가 되도록 변형해보기
5. 다양한 한붓그리기 문제 만들어보기
수학자 오일러는 쾨니히스베르크의 다리에서 한붓그리기 원리를 발견하였으며, 이는 현대 위상수학이라는 수학적 영역으로 확장되었다. 대표적으로 선과 점으로만 이루어진 지하철 노선도가 한붓그리기의 원리가 적용된 사례라 볼 수 있다.
이산수학, 위상수학, 대수학, 선형 대수학 등 수학이라는 학문은 여러 가지 어려운 정의와 이름으로 포장되었지만, 사실 수학은 우리주변의 작은 원리로부터 출발한 생활과 밀접한 학문이다.
제보는 카카오톡 haninpost 무단 전재-재배포 <금지>
카톡아이디 haninpost
