필자의 어릴 적 취미는 바둑이었다. 대학교 시절, 강의실에서 교수님 눈치를 피해가며 몰래 인터넷 바둑을 즐겨 두던 기억이 아직도 생생하다. 상대방 돌을 현혹하며, 끊임없이 세력을 확장해가는 ‘수많은 경우의 수’가 바둑이 지닌 매력적인 요소가 아닐까 생각한다.
정사각형 모양의 바둑판은 가로와 세로 각각 19줄로 되어 있다. 또 이 선들이 겹쳐서 만드는 점은 361개이다. 흑돌과 백돌이 361점 위의 적당한 지점에 서로 번갈아 한 번씩 돌을 놓으면서 바둑은 시작된다.
그렇다면 바둑에서 둘 수 있는 가지 수는 얼마나 될까?
처음에 두는 사람은 361 점을 마음대로 택할 수 있으니, 361개의 선택 가능성이 있다. 그렇다면, 그 다음 사람은 점 1개가 줄은 360개의 점을 둘 수 있게 된다. 이러한 원리를 반복해가면 다음과 같은 수식이 나온다.
<361 × 360 × 359 × (중간 생략) × 2 × 1>
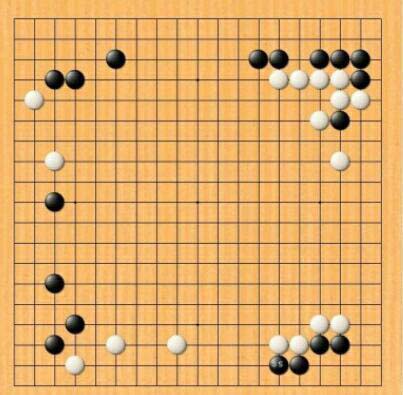 위 수식을 계산해보면, 지구상에 존재하는 모든 모래알 개수보다도 많은 ‘엄청난 경우’의 수가 나온다. 이 기나긴 식을 간단히 표현한 약속이 바로 361! (=361 팩토리얼) 이다.
위 수식을 계산해보면, 지구상에 존재하는 모든 모래알 개수보다도 많은 ‘엄청난 경우’의 수가 나온다. 이 기나긴 식을 간단히 표현한 약속이 바로 361! (=361 팩토리얼) 이다.
수학에서 361!과 같은 계승을 가장 많이 사용하는 것이 순열이다. 이는 컴퓨터로 계산하기에도 어마어마한 가짓수이며, 이렇게 복잡하고 변수가 많은 게임이 바로 바둑이인 것이다. 하지만 이렇게 복잡한 바둑에도 누구나 공감하는, 그리고 승리하기 위해 따라가야 할 ‘정석’과 ‘형마’가 있다.
수많은 변수와 불분명성이 존재하는 우리의 인생 또한 마찬가지이다. 바둑을 둘 때, 모든 것을 단지 운에만 맡기는 아무도 사람은 없다. 본인이 익힌 ‘정석’과 ‘형마’가 자신이 그릴 수 있는 바둑의 토대가 되기 때문이다.
따라서, 우리는 적절한 시기에 올바른 ‘정석’과 ‘형마’를 익혀야 한다. 우리의 인생도, 우리 교육의 방향도 이와 같이 변화해야 하지 않을까 생각한다.
이 기사가 정보에 도움이 되셨는지요? 기사는 독자 원고료로 만듭니다. 24시간 취재하는 10여 기자에게 원고료로 응원해 주세요. 한국 인도네시아 문의 카톡 아이디 haninpost
























![[연예] 엑소, 2026년 월드 투어 ‘엑소리즌’ 대장정 돌입… 6월 자카르타 입성](https://haninpost.com/wp-content/uploads/2026/02/월드-투어-콘서트-‘EXO-PLANET-6-–-EXhOrizon엑소-플래닛-6-엑소리즌-180x135.jpg)




![[기고문] “아세안 가입한 동티모르…한국과 동반성장 서사 만들길”](https://haninpost.com/wp-content/uploads/2025/10/최창원-고려대-아세아문제연구원-연구위원-238x178.jpg)





















 카톡아이디 haninpost
카톡아이디 haninpost

